How to draw and interpolate a B-spline curve on python

On this post,we will enumerate and compare drawing vs interpolating a B-spline curves

Requirements

Things you'll need:

Python 2.7.x or 3.x.x,
Numpy
Scipy
Matplotlib

Getting hands dirty

Assuming you already know a little about B-spline curves, if not just google about it or go here ^^.

Let consider a 9 points list named plist :

plist = [(3 , 1), (2.5, 4), (0, 1), (-2.5, 4),(-3, 0), (-2.5, -4), (0, -1), (2.5, -4), (3, -1),]

We will do two things :

A. Drawing a cubic B-Spline curve where plist is the control polygon. B. Find(interpolate) and draw the B-spline curve that go trough plist points and or in other words a curve fitting using a cubic B-spline curve.

As we will work with Numpy , let's create a numpy array named ctr form plist a split it to x and y arrays.

ctr =np.array(plist)

x=ctr[:,0]
y=ctr[:,1]

A. Drawing the B-spline Curve

We will draw a cubic B-spline which degree k=3 as it's the most used one. We need now to define the knots vector, with k ending equal knots:

l=len(x)
t=np.linspace(0,1,l-2,endpoint=True)
t=np.append([0,0,0],t)
t=np.append(t,[1,1,1])

Now we have defined all requirement to draw it. we can construct a sequence of length 3 containing the knots, coefficients, and degree of the spline to pass it as the tck argument to scipy.interpolate.splev , the function that will evaluate our curve:

tck=[t,[x,y],3]

And as we will evaluate the B-spline curve, we need a second parameter__u__ , an array of points :

u3=np.linspace(0,1,(max(l*2,70)),endpoint=True)

And we evaluate it :

out = interpolate.splev(u3,tck)

Drawing it using matplotlib :

Cubic B-spline curve drawing

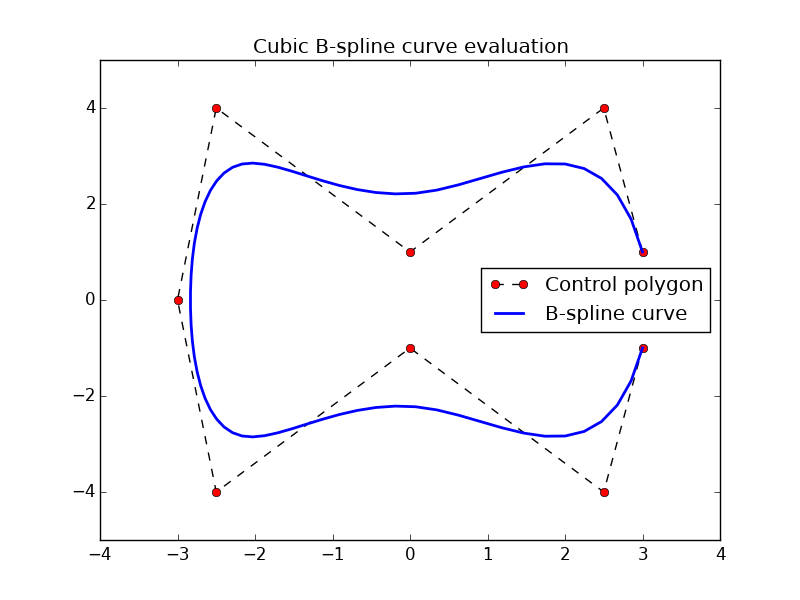
With this code :

plt.plot(x,y,'k--',label='Control polygon',marker='o',markerfacecolor='red')
plt.plot(out[0],out[1],'b',linewidth=2.0,label='B-spline curve')
plt.legend(loc='best')
plt.axis([min(x)-1, max(x)+1, min(y)-1, max(y)+1])
plt.title('Cubic B-spline curve evaluation')
plt.show()

B. interpolate the B-spline Curve

We will interpolate now the B-spline cruve that should go through n points. As we done before, a numpy array must be created using plist and split into x and y arrays :

plist = [(3 , 1), (2.5, 4), (0, 1), (-2.5, 4),(-3, 0), (-2.5, -4), (0, -1), (2.5, -4), (3, -1),]

ctr =np.array(plist)

x=ctr[:,0]
y=ctr[:,1]

To interpolate the B-spline that go through this points. To do so, we will be using scipy.interpolate.splprep, to get the interpolated S-pline parameters :

u,tck=interpolate.splprep([x,y],k=3,s=0)

And we use them to evaluate it using scipy.interpolate.splev, we still have a to redefine u variable to get a clear plot :

u=np.linspace(0,1,num=50,endpoint=True)
out = interpolate.splev(u,tck)

and we finaly draw it : Cubic B-spline curve interplation

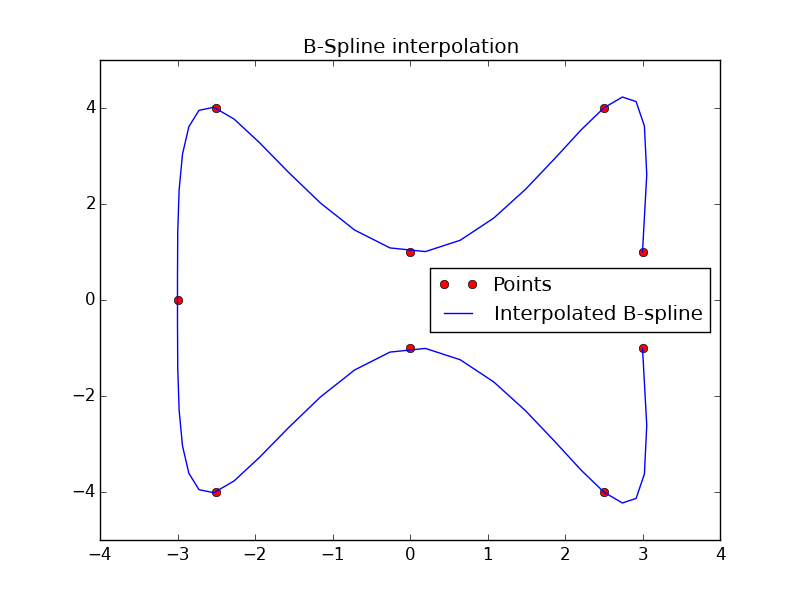
With this code :

plt.figure()
plt.plot(x, y, 'ro', out[0], out[1], 'b')
plt.legend(['Points', 'Interpolated B-spline', 'True'],loc='best')
plt.axis([min(x)-1, max(x)+1, min(y)-1, max(y)+1])
plt.title('B-Spline interpolation')
plt.show()

Full code :

B-Spline evalutation

import numpy as np
from scipy import interpolate

import matplotlib.pyplot as plt


ctr =np.array( [(3 , 1), (2.5, 4), (0, 1), (-2.5, 4),
                (-3, 0), (-2.5, -4), (0, -1), (2.5, -4), (3, -1),])
x=ctr[:,0]
y=ctr[:,1]

# uncomment both lines for a closed curve
#x=np.append(x,[x[0]])  
#y=np.append(y,[y[0]])

l=len(x)  

t=np.linspace(0,1,l-2,endpoint=True)
t=np.append([0,0,0],t)
t=np.append(t,[1,1,1])

tck=[t,[x,y],3]
u3=np.linspace(0,1,(max(l*2,70)),endpoint=True)
out = interpolate.splev(u3,tck)

plt.plot(x,y,'k--',label='Control polygon',marker='o',markerfacecolor='red')
#plt.plot(x,y,'ro',label='Control points only')
plt.plot(out[0],out[1],'b',linewidth=2.0,label='B-spline curve')
plt.legend(loc='best')
plt.axis([min(x)-1, max(x)+1, min(y)-1, max(y)+1])
plt.title('Cubic B-spline curve evaluation')
plt.show()

B-Spline interpolation

import numpy as np
from scipy import interpolate

import matplotlib.pyplot as plt

#x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
#y = np.sin(x)

ctr =np.array( [(3 , 1), (2.5, 4), (0, 1), (-2.5, 4),
                (-3, 0), (-2.5, -4), (0, -1), (2.5, -4), (3, -1)])

x=ctr[:,0]
y=ctr[:,1]

#x=np.append(x,x[0])
#y=np.append(y,y[0])

tck,u = interpolate.splprep([x,y],k=3,s=0)
u=np.linspace(0,1,num=50,endpoint=True)
out = interpolate.splev(u,tck)

plt.figure()
plt.plot(x, y, 'ro', out[0], out[1], 'b')
plt.legend(['Points', 'Interpolated B-spline', 'True'],loc='best')
plt.axis([min(x)-1, max(x)+1, min(y)-1, max(y)+1])
plt.title('B-Spline interpolation')
plt.show()

Thanks to give your feedback in a comment and help me improve this article.